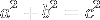Pythagorean theorem

A visual explanation by Victor Powell for Setosa

What follows in an interactive walk through of Euclid's proof of the Pythagorean Theorem.

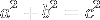
Let ABC be a right-angled triangle having the angle BAC right.

I say that the square on BC equals the sum of the squares on BA and AC.

Describe the square BDEC on BC, and the squares GB and HC on BA and AC. Draw AL through A parallel to either BD or CE, and join AD and FC.

Since each of the angles BAC and BAG is right, it follows that with a straight line BA, and at the point A on it, the two straight lines AC and AG not lying on the same side make the adjacent angles equal to two right angles, therefore CA is in a straight line with AG.

For the same reason BA is also in a straight line with AH.

Since the angle DBC equals the angle FBA, for each is right, add the angle ABC to each, therefore the whole angle DBA equals the whole angle FBC.

Since DB equals BC, and FB equals BA, the two sides AB and BD equal the two sides FB and BC respectively, and the angle ABD equals the angle FBC, therefore the base AD equals the base FC, and the triangle ABD equals the triangle FBC.

Now the parallelogram BL is double the triangle ABD, for they have the same base BD and are in the same parallels BD and AL. And the square GB is double the triangle FBC, for they again have the same base FB and are in the same parallels FB and GC.

Therefore the parallelogram BL also equals the square GB.

Similarly, if AE and BK are joined, the parallelogram CL can also be proved equal to the square HC. Therefore the whole square BDEC equals the sum of the two squares GB and HC.

And the square BDEC is described on BC, and the squares GB and HC on BA and AC.

Therefore the square on BC equals the sum of the squares on BA and AC.

Therefore in right-angled triangles the square on the side opposite the right angle equals the sum of the squares on the sides containing the right angle..

Text from Euclid's Elements, Proposition 47